Probabilistic and Bayesian Matrix Factorizations for Text Clustering
Natural language processing is in a curious place right now. It was always a late bloomer (as far as machine learning subfields go), and it’s not immediately obvious how close the field is to viable, large-scale, production-ready techniques (in the same way that, say, computer vision is). For example, Sebastian Ruder predicted that the field is close to a watershed moment, and that soon we’ll have downloadable language models. However, Ana Marasović points out that there is a tremendous amount of work demonstrating that:
“despite good performance on benchmark datasets, modern NLP techniques are nowhere near the skill of humans at language understanding and reasoning when making sense of novel natural language inputs”.
I am confident that I am very bad at making lofty predictions about the future. Instead, I’ll talk about something I know a bit about: simple solutions to concrete problems, with some Bayesianism thrown in for good measure!
This blog post summarizes some literature on probabilistic and Bayesian matrix factorization methods, keeping an eye out for applications to one specific task in NLP: text clustering. It’s exactly what it sounds like, and there’s been a fair amount of success in applying text clustering to many other NLP tasks (e.g. check out these examples in document organization, corpus summarization and document classification).
What follows is a literature review of three matrix factorization techniques for machine learning: one classical, one probabilistic and one Bayesian. I also experimented with applying these methods to text clustering: I gave a guest lecture on my results to a graduate-level machine learning class at The Cooper Union (the slide deck is below). Dive in!
Non-Negative Matrix Factorization (NMF)
NMF is a very well-known matrix factorization technique, perhaps most famous for its applications in collaborative filtering and the Netflix Prize.
Factorize your (entrywise non-negative) $m \times n$ matrix $V$ as $V = WH$, where $W$ is $m \times p$ and $H$ is $p \times n$. $p$ is the dimensionality of your latent space, and each latent dimension usually comes to quantify something with semantic meaning. There are several algorithms to compute this factorization, but Lee and Seung’s multiplicative update rule (originally published in NIPS 2000) is most popular.
Fairly simple: enough said, I think.
Probabilistic Matrix Factorization (PMF)
Originally introduced as a paper at NIPS 2007, probabilistic matrix factorization is essentially the exact same model as NMF, but with uncorrelated (a.k.a. “spherical”) multivariate Gaussian priors placed on the rows and columns of $U$ and $V$. Expressed as a graphical model, PMF would look like this:

Note that the priors are placed on the rows of the $U$ and $V$ matrices.
The authors then (somewhat disappointing) proceed to find the MAP estimate of the $U$ and $V$ matrices. They show that maximizing the posterior is equivalent to minimizing the sum-of-squared-errors loss function with two quadratic regularization terms:
$$ \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{M} {I_{ij} (R_{ij} - U_i^T V_j)^2} + \frac{\lambda_U}{2} \sum_{i=1}^{N} |U|_{Fro}^2 + \frac{\lambda_V}{2} \sum_{j=1}^{M} |V|_{Fro}^2 $$
where $|\cdot|_{Fro}$ denotes the Frobenius norm, and $I_{ij}$ is 1 if document $i$ contains word $j$, and 0 otherwise.
This loss function can be minimized via gradient descent, and implemented in your favorite deep learning framework (e.g. Tensorflow or PyTorch).
The problem with this approach is that while the MAP estimate is often a reasonable point in low dimensions, it becomes very strange in high dimensions, and is usually not informative or special in any way. Read Ferenc Huszár’s blog post for more.
Bayesian Probabilistic Matrix Factorization (BPMF)
Strictly speaking, PMF is not a Bayesian model. After all, there aren’t any priors or posteriors, only fixed hyperparameters and a MAP estimate. Bayesian probabilistic matrix factorization, originally published by researchers from the University of Toronto is a fully Bayesian treatment of PMF.
Instead of saying that the rows/columns of U and V are normally distributed with zero mean and some precision matrix, we place hyperpriors on the mean vector and precision matrices. The specific priors are Wishart priors on the covariance matrices (with scale matrix $W_0$ and $\nu_0$ degrees of freedom), and Gaussian priors on the means (with mean $\mu_0$ and covariance equal to the covariance given by the Wishart prior). Expressed as a graphical model, BPMF would look like this:
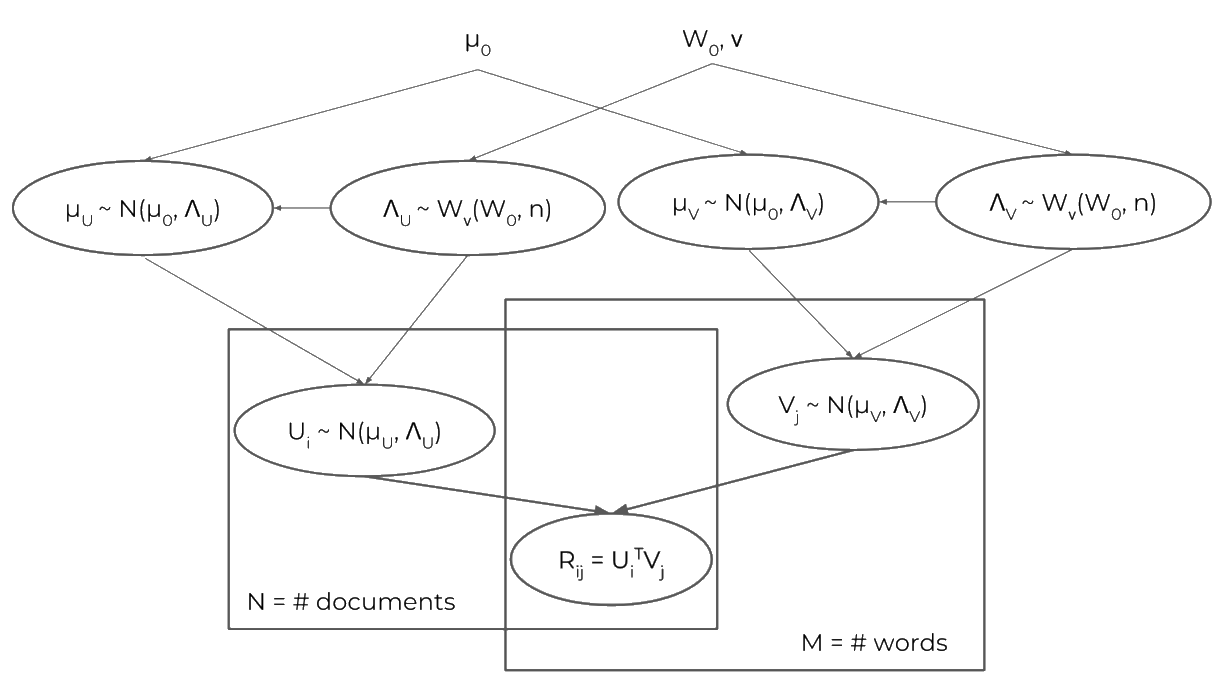
Note that, as above, the priors are placed on the rows of the $U$ and $V$ matrices, and that $n$ is the dimensionality of latent space (i.e. the number of latent dimensions in the factorization).
The authors then sample from the posterior distribution of $U$ and $V$ using a Gibbs sampler. Sampling takes several hours: somewhere between 5 to 180, depending on how many samples you want. Nevertheless, the authors demonstrate that BPMF can achieve more accurate and more robust results on the Netflix data set.
I would propose two changes to the original paper:
- Use an LKJ prior on the covariance matrices instead of a Wishart prior. According to Michael Betancourt and the PyMC3 docs, this is more numerically stable, and will lead to better inference.
- Use a more robust sampler such as NUTS (instead of a Gibbs sampler), or even resort to variational inference. The paper makes it clear that BPMF is a computationally painful endeavor, so any speedup to the method would be a great help. It seems to me that for practical real-world applications to collaborative filtering, we would want to use variational inference. Netflix ain’t waiting 5 hours for their recommendations.
Application to Text Clustering
Most of the work in these matrix factorization techniques focus on dimensionality reduction: that is, the problem of finding two factor matrices that faithfully reconstruct the original matrix when multiplied together. However, I was interested in applying the exact same techniques to a separate task: text clustering.
A natural question is: why is matrix factorization1 a good technique to use for text clustering? Because it is simultaneously a clustering and a feature engineering technique: not only does it offer us a latent representation of the original data, but it also gives us a way to easily reconstruct the original data from the latent variables! This is something that latent Dirichlet allocation, for instance, cannot do.
Matrix factorization lives an interesting double life: clustering technique by day, feature transformation technique by night. Aggarwal and Zhai suggest that chaining matrix factorization with some other clustering technique (e.g. agglomerative clustering or topic modelling) is common practice and is called concept decomposition, but I haven’t seen any other source back this up.
I experimented with using these techniques to cluster subreddits (sound familiar?). In a nutshell, nothing seemed to work out very well, and I opine on why I think that’s the case in the slide deck below. This talk was delivered to a graduate-level course in frequentist machine learning.
Probabilistic and Bayesian Matrix Factorizations for Text Clustering
I experimented with using these techniques to cluster subreddits. In a nutshell, nothing seemed to work out very well, and I opine on why I think that’s the case in this slide deck. This talk was delivered to a graduate-level course in frequentist machine learning.
which is, by the way, a severely underappreciated technique in machine learning ↩︎